Das Geheimnis des "Map Datums"

Jeder, der mit Landkarten navigiert, sei es manuell oder mit GPS, kennt das Problem: Legt man das falsche Map Datum (im Deutschen leider recht unglücklich als Kartendatum bezeichnet) zugrunde, kann es bei der Ermittlung der Koordinaten zu recht großen Abweichungen kommen. Und das richtige Map Datum zu finden, kann recht spannend und nervenaufreibend werden, denn auf vielen Landkarten fehlen die Angaben hierzu.

Die Erde - Eine KartoffelDoch was verbirgt sich hinter dem Zauberbegriff "Map Datum"? Viele werfen mit dem Begriff um sich und bei Nachfragen wird dann noch was von Bezugssystem gemurmelt und damit hat es sich auch meistens - mehr ist nicht! Aber der Begriff ist schnell entzaubert, wenn man weiß, worum es geht.

Ein wenig Theorie muss sein

Was ist die Erde? Da hatten unsere Vorfahren so ihre Vorstellungen:

Eine Scheibe? Eine Kugel? Ein Ellipsoid? Leider ist sie keins von allem. Eigentlich ist sie mit "eine Kartoffel" am besten beschrieben und diese spezielle Kartoffel wird als Geoid bezeichnet.

Da braucht man kaum Kenntnisse in angewandter Geometrie, um sich auszumalen, wie schwierig es werden kann, wenn man die Koordinaten eines Punktes auf der Erdoberfläche berechnen will. Da hat man sich in Vorzeiten so allerlei einfallen lassen:

Man nahm einen Ellipsoiden (so eine Art Rugbyball) als Idealfigur der Erde (mit dem konnte man nämlich gut rechnen). Da man nun nicht immer die ganze Erde auf einer Landkarte darstellen musste, hatte man festgestellt, dass je nach Gegend mal der eine, mal der andere Ellipsoid besser passte.

Viele Ellipsoiden führen zum ZielZur Veranschaulichung haben wir hier an unserer Kartoffel mal zwei Ellipsoiden angebracht. Der Blaue passt ganz gut in beiden Polregionen, während z.B. der Rote im Norden für einen größeren Bereich noch besser passt.

Und so kam es, dass die nationalen Vermessungsämter unterschiedliche Ellipsoiden benutzten und auch heute noch benutzen. Hier die Namen von einigen solchen Ellipsoiden: Bessel 1841, International 1924, Helmert 1906, ... Übrigens - es gibt auch einen Ellipsoiden WGS84, der für das Map Datum WGS84 benutzt wird - wie auch WGS72 für das gleichnamige Map Datum. Aber das sind Ausnahmen, denn ansonsten haben die zugrunde liegenden Ellipsoiden und die darauf beruhenden Map Datums unterschiedliche Namen.

Mit der Festlegung des Ellipsoiden ist aber in jedem Fall der erste Schritt zur Festlegung des Map Datums getan!

Schauen wir uns so einen Ellipsoiden näher an:Das Aussehen des Ellipsoiden ist bestimmt durch die Länge der kurzen Achse (blau, in Formeln als b bezeichnet) und die Länge der langen Achse (schwarz, in Formeln als a bezeichnet). Das Verhältnis der beiden Achsen legt fest, ob es sich um einen flachen "Fladen" (kurze Achse ganz kurz, lange Achse ganz lang) oder ob es sich z.B. um eine Kugel handelt (beide Achsen gleich lang) und wird Abplattung genannt (in Formeln als f bezeichnet - für englisch: flattening mit f= (a-b)/a). Der flache "Fladen" hat eine größere Abplattung (ist platter) als z.B. die Kugel.

Auf die Achsen kommt es an! Das Zentrum der Erde ....

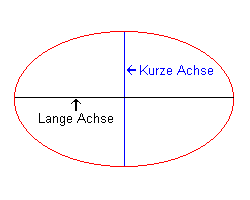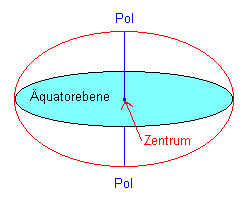Die kurze Achse verbindet die beiden Pole, die lange Achse liegt auf Höhe des Äquators. Beide Achsen gehen durch den Erdmittelpunkt, das Zentrum.

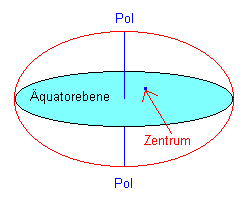liegt nicht immer da, wo wie es erwartenBis jetzt haben wir ein schönes "Weltbild" aufgebaut, das für die Ellipsoiden WGS84 und WGS72 auch stimmt.

Aber es gibt eben auch Ellipsoiden, mit denen die Vermesser nicht ganz zufrieden waren und so griffen sie zu einem Trick: Sie verschoben einfach das Zentrum der Erde für ihre Bedürfnisse und schon konnten sie einfacher rechnen für genauere Landkarten. Die Rechnerei ist kompliziert und hier unwichtig, einfacher ist es, man schaut es sich in unseren Bildern an!

Nun kramen wir ganz tief in unseren Geometriekenntnissen aus der Schulzeit: Jeder Punkt in einem dreidimensionalen Objekt ist durch 3 Koordinaten bestimmt: X, Y, Z.

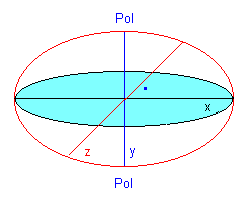X Y Z legen jeden Punkt festDer Ursprung ist durch X=0, Y=0, Z=0 bestimmt. Z.B. bei WGS84 ist das unser Zentrum.

Wurde das Zentrum verschoben, gibt man diese Verschiebung in Metern an, so z.B. X=110 m, Y=90 m, Z=41 m. Diese Verschiebung kann auch negativ sein.

Wird z.B. das Zentrum nach Süden verschoben, dann wird Y negativ, bei einer Verschiebung nach Westen wird X negativ. Mit der Ermittlung der geometrischen Koordinate des Zentrums haben wir den zweiten und letzten Schritt zur Festlegung unseres Map Datums getan.

Nicht immer ist der Name des Map Datums eindeutig, wie wir in unseren nachfolgenden Beispielen für European 1950 sehen. Wir müssen dabei immer wissen, für welche Region das Map Datum gültig ist.

Beispiele:

Map Datum Ellipsoid X Y Z Einsatzgebiet
WGS84 WGS84 0 0 0 weltweit
Massawa Bessel 1841 639 405 60 Äthiopien
European 1950 International 1924 -112 -77 -145 Tunesien
European 1950 International 1924 -84 -107 -120 Portugal, Spanien

Um es nochmal kurz zusammenzufassen:

Das Map Datum ist bestimmt durch den Ellipsoiden und die geometrischen Koordinaten des Zentrums.

Konvertierung ist keine Hexerei

In der Regel müssen wir uns bei Verwendung von GPS-Empfängern oder GPS-Software wie Fugawi wenig Gedanken machen um die Einstellung von Map Datums. Voreingestellt ist WGS84 und viele neuen Karten basieren auf WGS84. Im GPS oder in der Software wird eine riesige Menge an weiteren Map Datums angeboten, aus der man auswählen kann. Doch was ist zu tun, wenn das Map Datum fehlt?

In diesem Fall müssen wir für das fehlende Map Datum ein sogenanntes User Datum definieren, das durch 5 Parameter festgelegt wird: da, df, dx, dy, dz. Wenn wir Glück haben, finden wir alle Parameter z.B. in der Garmin-Tabelle und brauchen gar nichts mehr weiter zu ermitteln. Wir können diese Parameter dann direkt (z.B. beim GPS 12XL) unter Setup-Menü -> Navigation (Nav Setup) -> Map Datum -> User eingeben.

Die Parameter dx, dy und dz sind identisch mit den geometrischen Koordinaten unserer Zentrumsverschiebung und können (zusammen mit dem zugrunde liegenden Ellipsoiden) direkt aus verfügbaren Tabellen (wie z.B. aus Quellen des DoD) entnommen werden. Um die noch fehlenden Werte da und df zu berechnen, brauchen wir ergänzend eine Tabelle mit den benötigten Ellipsoid-Daten.

Der Parameter da ist in den Garmin-Tabellen die Differenz zwischen der halben langen Achse des WGS84 Ellipsoiden (a/2 = 6378137) und der halben langen Achse des Ellipsoiden, der dem gesuchten Map Datum zugrunde liegt:

da = a/2WGS84 - a/2Ellipsoid

Der Parameter df ist die Differenz zwischen Abplattung des WGS84 Ellipsoiden (f = 0,003352810665) und Abplattung des Ellipsoiden, der dem gesuchten Map Datum zugrunde liegt, multipliziert mit 10.000:

df = (fWGS84 - fEllipsoid) * 10.000

Soweit ist für das User Datum nun alles definiert und wir können es im GPS oder in unserer Software erfassen.

Zur Verdeutlichung der Notwendigkeit und des Verfahrens im folgenden ein Beispiel anhand unserer bei Slowenien 99 verwendeten Karte.

Das Map Datum der Karte 1:50.000 war unbekannt, also setzten wir WGS84 voraus und nahmen unterwegs einen Punkt mit dem GPS (Tour 3, "Gostice Planinski Dom", Roadbook Wegpunkt 8):

  • N46°18,99599' E014°08,01664'

Beim Einzeichnen des Punkts in die Karte lag dieser ca. einen Zentimeter zu weit westlich (siehe Leserforum GPS). Alle weiteren Versuche, das Map Datum zu "erhacken", schlugen fehl. Die Antwort des slowenischen Vermessungsamts (in Deutsch!) auf eine diesbezügliche Anfrage half jedoch weiter. Basis wäre der Bessel-Ellipsoid, mehr Informationen gab es aber nicht aus Lubljana. Wir forschten mit dieser Information weiter und fanden das Datum Hermannskogel, das für Jugoslawien benutzt wurde und auf dem Bessel-Namibia Ellipsoiden basiert, in unserer bereits oben erwähnten Tabelle.

Direkt entnommen werden können dieser Tabelle die Werte für Hermannskogel dx = 653, dy = -212 und dz = 449.
Bleiben noch die ausstehenden Werte für da und df, die lassen sich nach der obigen Formel wie folgt errechnen, indem man die Werte für den Hermannskogel zugrunde liegenden Ellipsoiden Bessel 1841 (Namibia) (siehe dazu auch die Lesermail unten von 01/02) aus unserer obigen Tabelle der Ellipsoid-Daten entnimmt: a/2 = 6377483,865 und f = 0,003342773182.

Damit ergibt sich für da und df nach unseren obigen Formeln:

da = 6378137 - 6377483,865 = 653,135
df = (0,003352810665 - 0,003342773182) * 10.000 = 0,10037483

Damit haben wir das Map Datum Hermannskogel vollständig als User Datum definiert mit:

dx = 653
dy = -212
dz = 449
da = 653,135
df = 0,10037483

Dies können wir nun problemlos in unser Garmin GPS eingeben, das die Umrechnung unserer obigen Koordinate wie folgt durchführt. Unser Wegpunkt 8 hat in der slowenischen 1:50.000er Karte damit plötzlich die Koordinaten

  • N46°19,01972´ E014°08,30101'.

Beim Einzeichnen des Punktes in die Landkarte gab es Jubel - nun saß er im wahrsten Sinne des Wortes: Punktgenau!

Noch eine Anmerkung zum Schluss: Einige werden nun sagen: "Tja, Map Datum, das ist schon wichtig, aber die Grids!". Nun, zu den Grids sagen wir auch etwas, dazu nur soviel an dieser Stelle: Map Datum und Grid sind zwei (fast beliebig) kombinierbare Systeme ...

(02/00) Zu unserem obigen Beitrag erhielten wir u.a. folgende Leseranfrage von Anton Volmer:

Hallo,
entweder habe ich folgenden Satz (Seite 3, unter der Tabelle) falsch verstanden, oder er ist so nicht richtig: "Das Map Datum ist bestimmt durch den Ellipsoiden und die geometrischen Koordinaten des Zentrums." Wie kann dann, in der Tabelle davor, das gleiche Map Datum für unterschiedliche Zentrumskoordinaten stehen?

An dieser Stelle liegt tatsächlich ein Missverständnis unseres Lesers vor:

Der "Name" des Map Datums ist nicht eindeutig (siehe "European 1950"). Wir müssen deshalb immer wissen, für welche "Region" das Map Datum gültig ist und gegebenenfalls im GPS bzw. in der Navigations-Software anstatt "European 1950" ein User Datum einstellen.

Beispiele:

1. Wir haben eine Landkarte von Deutschland und finden den Vermerk "European 1950". Dann können wir beim Garmin-GPS als Map Datum "European 1950" einstellen, das mit Ellipsoid "International 1924" und mit dx= -87, dy= -96 dz= -120 definiert ist (kann man in diesem Fall zufällig aus der bei uns veröffentlichten Garmin-Tabelle entnehmen, auch wenn der Ellipsoid dabei unbekannt bleibt - ansonsten muss man die Einstellung im Zweifel bei Garmin erfragen).

2. Wir haben eine Landkarte von Tunesien und finden den Vermerk "European 1950". Hier werden wir mit der Einstellung "European 1950" im Garmin-GPS Probleme bekommen. Folglich empfiehlt es sich, stattdessen ein User Datum einzustellen mit dx= -112, dy= -77, dz= -145 (Einstellung lt. der bei uns veröffentlichten Tabelle gemäß DoD).

Wenn man in die letztere Tabelle schaut, stellt man fest, dass sogar für Deutschland 2 Einträge mit "European 1950" vorhanden sind, einmal dx= -87, dy= -96 dz= -120 und dann noch dx= -87, dy= -98, dz= -121. Da muss man dann wohl oder übel "rumprobieren": Zuerst mit dem Garmin-Standard European 1950 und falls das nicht passt, mit dem User Datum.

Es ist also schon zutreffend, dass ein Map Datum nicht durch seinen Namen, sondern durch den Ellipsoiden und die geometrischen Koordinaten des Zentrums definiert ist.

(06/01) Sehr gefreut haben wir uns über die Mail von G. Besmer, da wir mit diesem Thema offenbar inspirierend bis nach Madagaskar gewirkt haben:

Liebes Explorer Team,

inspiriert von Eurer Internet Seite, haben wir zusammen mit dem oertlichen geographischen Institut die GPS Parameter fuer die Labord Koordinaten bestimmt. Die Parmeter fuer das Labord Koordinatennetz (1000 m Merkatorgitter) haben fuer das Zentrum vom Madagaskar gute Resultate erbracht, waehrend in den Randzonen mit geringen Abweichung zu rechen ist (Provinz Majunga x = ok, y = -40 m systematisch). Immerhin schon ein recht gutes Resultat. Weitere Gelaendetests sind in Gange.

Hier folgend die verwendeten Parameter:

Usergrid:

Longitude origine = 46°26.140 Est (centre de la projection par rapport à Greenwich)
Scale = 0.9995 (facteur d'échelle)
False Easting (m) = 399 835.6
False Northing (m) = 2 889 585.8

Map Datum:

Datum Ellipsoid dX dY dZ Einsatzgebiet
Tananarive Observatory 1925 International 1924
dx= -189
dy= -242
dz= -91
Madagascar

Berechnung (in m):

da = a/2WGS84 - a/2 Ellipsoid (WGS84 Ellipsoiden (a/2 = 6378137))
df = (fWGS84 - fEllipsoid) * 10.000 (WGS84 Ellipsoiden (f = 0,003352810665))
a/2 Ellipsoid International 1924 = 6378388,000
fEllipsoid International 1924 = 0,003367003367 (1/Abplattung =297,000000000)
delta a GPS = 6378137-6378388,000 = -251
delta f GPS = (0,003352810665-0,003367003367)*10 = -0,000141927

Es gilt noch einmal festzuhalten, dass die vorliegenden Daten im Zentralenhochland zu genauen Resultaten fuehren und als erster Versuch zu werten sind. Informationen ueber Tests in anderen Zonen sind wuenschenwert, und koennten zu Parameterangaben zum Usergrid fuer verschiedene Zonen fuehren.

Mit Gruss
G. Besmer
PDFIV Gesellschaft fuer Technische Zusammenarbeit (GTZ),
Ambatolampy Madagaskar

(01/02) Unser Leser Markus Adam hat sich noch einmal genauer befasst mit dem erwähnten Ellipsoiden Bessel 1841 und hat dabei Interessantes heraus gefunden:

Sehr geehrtes Explorerteam,

mit Interesse habe ich Ihren Artikel "Das Geheimnis des Map Datums" in Ihrem Online-Magazin gelesen, da ich letztes Jahr erstmalig als Skipper in Kroatien mit einer Segelyacht unterwegs war und somit mit dem Mapdatumproblem konfrontiert wurde.

Bei weiteren Recherchen bin ich auf eine Internetseite des "Department of Defense" gelangt, wonach das Datum Herrmannskogel aus Ihrem Beispiel auf dem Ellipsoiden Bessel 1841 (Ethiopien, Indonesien, Japan und Korea) und nicht auf Bessel 1841 (Namibia) basiert [Quelle S.94 A.1-1 und S.150 C.1-1]. Weiterhin ist der Veröffentlichung folgendes User Datum für die Region Slowenien und Kroatien zu entnehmen [S.153 C.2-2]:

dx= 682 m
dy=-203 m
dz= 480 m
da= 739,845 m
df= 0,10037483

Das Koordinatenbeispiel mit Wegepunkt 8 in Slowenien ergibt nach Standard Molodensky Transformation die Position N46°19,01999' E14°08,29973'. Zugegeben, die Abweichung zu Ihrer Position beträgt weniger als 2 m, was sowieso unter der Genauigkeit eines billigen GPS Handempfängers liegt, jedoch sollen obige Werte angeblich für das ganze ehemalige Gebiet von Jugoslawien gelten. Beim nächsten Segeltörn in Kroatien werde ich ausprobieren, welche Einstellungen die besseren sind.

Mit freundlichen Grüßen
Markus Adam

Quelle:
NIMA Technical Report TR8350.2, "Department of Defense World Geodetic System 1984,
Its Definition and Relationships With Local Geodetic Systems", Third Edition

Zwar legen diverse Quellen für Hermannskogel Bessel 1841 Namibia zu Grunde, aber Markus Adam hat Recht: Im Anhang des Field Manual 6 wird Bessel 1841 (entspricht dem von unserem Leser genannten) für Jugoslawien angenommen. In anderen Quellen (z.B. zur Neuordnung des Vermessungswesens im Kosovo) wird ebenfalls Bessel 1841 für Hermannskogel benutzt. Auch das Bundesamt für Eich- und Vermessungswesen in Wien legt für Hermannskogel Bessel 1841 zugrunde. Ausgehend davon, dass es sich um ein österreichisches Kartendatum handelt, schließen wir uns deshalb der obigen Meinung an.

(09/02) Und noch mehr Fakten zum Thema "Hermannskogel" sowie der Kartografie im ehemaligen Jugoslawien stellte unser Leser Achim Brönner zusammen:

Sehr geehrtes Explorteam, werte Mitexplorer,

die Beiträge über das Datum Herrmannskogel waren sehr hilfreich für die Arbeit im Bereich des ehemaligen Jugoslawien. Die dortigen Messtischblätter 1:25.000 stammen zwar aus der Zeit vor 1990 (meist mit Aktualisierungsstand Ende 70er und 80er Jahre), sind aber heute immer noch die gebräuchlichen topographischen Karten. Diese Karten tragen die Angabe Gaus-Krigerova projekcija und zeichnen sich durch ein 4 cm Gitter und 7-stellige Meterkoordinaten aus (die Blattecken sind mit geogr. Koordinaten bezeichnet). Dies ist ein auch von den (West-) Deutschen Kartenblättern vertrautes Bild.

Wie arbeitet man nun im Gelände mit diesen Karten und dem GPS? Es stellt sich unweigerlich die leidliche Frage nach Map Datum und Map Grid und den am GPS einzustellenden Parametern.

Ein kurze Überlegung zum deutschen Gauss-Krüger System hilft weiter: Beim GPS wären, wenn man nicht das vorgegebene German Grid und das Datum Potsdam wählt (Garmin), folgende Parameter zur Transformation aus dem WGS84 einzustellen:

Im Bereich zwischen 6° und 15° West gilt das Potsdam Datum (DHDN Rauenberg mit Bessel 1841), also

User Map Datum: dx = 606; dy = 23; dz = 413; da = 739.845; df = 0.10037483

Es bleibt das Geheimnis des Potsdam Datums, warum sich für diese Parameter nur spärlich Quellen finden lassen. Eine der wenigen Fundstellen neben dem Explorer Magazin ist die Aufstellung von Dana, Univ. Texas [1].

Für das Kartengitter muss bei Benutzer-Eingabe nach der geographischen Länge unterschieden werden. Hier sind beispielsweise für Mittelmeridian 9° Ost (gilt etwa für Hamburg, Hannover, Frankfurt, Stuttgart), also GK-Zone Kennziffer 3 folgende Einstellungen zu machen:

User Grid:

  • Longitude of Origin: E 009° 00.000'
  • False Easting: 3500000.0 m
  • Scale: 1.000000 (d.h. längentreuer Mittelmeridian)
  • False Northing: 0.0 m.

Es liegt nun nahe, dieses Parametermuster auf das jugoslawische Gaus-Krigerova System anzuwenden, das dort 1924 eingeführt wurde [2]. Der Anwendungsbereich des Gauss-Krüger Systems reicht bis zum 21. Längengrad Ost als Mittelmeridian, also GK-Meridianstreifenzone7.

Es gilt das Datum Herrmannskogel (Bessel 1841) mit den Werten, wie sie in den Beiträgen im Explorer Magazin genannt wurden und aus dem NIMA Technical Report zum WGS84 [3] stammen (also dx = 682m; dy = -203m; dz = 480 m; da = 739.845m; df = 0.10037483).

Mittlerweile wird von Garmin in der Auswahlliste ein Datum namens Croatia angeboten, das zu den gleichen Ergebnissen führt. Für das Kartengitter muss wieder die östl. Länge berücksichtigt werden, hier für das Beispiel Skopje, heutige Republik Mazedonien. Dieses liegt im GK-Meridianstreifen mit dem Mittelmeridian 21°Ost (d.h. in der GK-Zone 7).

User Grid:

  • Longitude of Origin: E 021° 00.000'
  • False Easting: 7500000.0 m
  • False Northing: 0.0 m

Für den Maßstab des Mittelmeridians muss der Wert 0.9999 eingegeben werden, da sonst die GK Hochwerte mehrere hundert Meter zu weit nördlich zu liegen kommen. Diese Angabe findet sich auch in dem Tagungsbeitrag zur Neuordnung des Katasterwesens im Kosovo [2], der bereits im Explorer Magazin zuvor erwähnt wurde.

Achim Brönner, Diplom Geograph

Quellenhinweise:

  1. Dana; P.H., Dept. Of Geography, Univ. of Texas, Austin 1997 (http://www.colorado.edu/geography/gcraft/notes/datum/dlist.html)
  2. Valstad 2001 (http://www.ddl.org/figtree/pub/proceedings/nairobi/valstad/TS17-2.pdf)
  3. National Imagery and Mapping Agency; TR8350.2, 3rd Edition Jan 2000 (Appendix C.2)

Ein Nachtrag von Achim Brönner folgte später noch:

Ich komme gerade wieder aus Jugoslavien, Montenegro, um genau zu sein. Auch dort klappt es mit den Benutzereinstellungen für Datum und Grid wie beschrieben (außer, dass diesmal GK Zone 6 wg. 18 Grad Ost einzustellen war und entsprechend 6500000 meter false Easting).

Auch ist das Garmin "Croatia" Datum offensichtlich identisch mit dem als User Grid eingestellten Herrmannskogel.

(02/02) Und noch eine weitere Anmerkung von unserem Leser Dr. Erich H. Meier, die sich auf die in unserem Beitrag erwähnte Tabelle bezieht:

Sehr geehrte Damen und Herren,

mit Interesse habe ich Ihre Seiten zu den Themen GPS und Referenzsysteme durchgeschaut. Herzlichen Dank fuer das Bereitstellen solcher Informationen.

Bei der Tabelle ist jedoch eine Frage aufgetaucht: Auf welches globale Referenzsystem beziehen sich die angegebenen Shift-Parameter? Auf WGS84, WGS72 oder eines der ITRFs? Und wenn letzteres: Auf welche Epoche?

Fast zu unterst in der Tabelle sieht man sowohl fuer WGS84 als auch fuer WGS72 den Shift 0 (Null). Dies kann nicht ganz stimmen, da diese 2 Systeme sich in der Z-Komponente um 4.5 m unterscheiden. Eine praezise Angabe des globalen Referenzsystems sowie der Transformationsrichtung waere noch hilfreich. Nichts desto trotz ist Ihre Tabelle eine Fundgrube!

Dr. Erich H. Meier
Remote Sensing Laboratories
University of Zurich-Irchel

Das Map Datum WGS72 hat auch den Ellipsoiden WGS72 als Grundlage. Bezogen auf diesen Ellipsoiden ergibt sich für dieses Bezugssystem keinerlei Verschiebung. Das gleiche trifft auch zu für z.B. North American 1983 / Canada mit dem Ellipsoid GRS 80, auch dort ist im Bezugssystem keine Verschiebung erforderlich.

Die Verschiebung bezieht sich immer auf den zugrunde gelegten Ellipsoiden und nicht auf ein "globales" Referenzsystem. Es ist korrekt, dass sich die Ellipsoiden WGS84 und WGS72 unterscheiden, dies ist z.B. bei der Umrechnung von WGS72 Koordinaten nach WGS84 zu berücksichtigen.

© 1999 - 2002 S. Zerlauth